What is the quantum model?

WHAT IS THE QUANTUM MODEL: BOHR MODEL

What is the quantum model? The quantum model is a conceptual framework of the atom informed by quantum physics. The predecessor to it was the Bohr model.

It states that electrons are only allowed in the specified orbitals (the concentric circles) above. Electrons are moving in circular orbits in their respective orbitals (orbits & orbitals get it?). However, orbitals are much more complex than this as you will soon see.

what is the quantum model: quantum model

First, we need to talk about the De Broglie Wavelength. λ=h/p where λ = De Broglie Wavelength, p = particle’s wavelength, and h = plank’s constant 6.626*10-23 J*s (the most important number in quantum physics where J=Joules and s=seconds). If λ is sufficiently small, then we observe quantum mechanics and wave properties. It must be around the nanometer scale.

what is the quantum model: Schrodinger's equation

Since it has wave-like properties, physicists use a wave equation called Schrodinger Equation to calculate these particles’ properties. The equation in its simplest form is as follows: HΨ = EΨ where Ψ is the wave function. The Hamiltonian (H) acts on the wave function (Ψ). When doing so, it gives you the energy (E) associated with the wave function along with the original wave function. Let’s look at an example wave function below.

Ψ = √(1/3)ψ1 +√(1/3)ψ2 +√(1/3)ψ3

We know that HΨ = EΨ. That is, when the Hamiltonian acts on a wave function, you get the energy along with the function. However, it’s also important to note that the Hamiltonian also acts on the “smaller” functions too. In essence, H1Ψ1 = E1Ψ1, H2Ψ2 = E2Ψ2, H3Ψ3 = E3Ψ3. To summarize, when the Hamiltonian acts on the 3 wave functions, you get 3 different energies each associated with their respective wave functions. Thus, the quantum particles represented by Ψ can only have energies E1, E2, and E3. The probability that it’ll have each of these energies is the square of the coefficients which is (√(1/3))2 = 1/3 for each of these energies. It’s the same probability that the quantum state will be either Ψ1 Ψ2 Ψ3. The Hamiltonian is a mathematical operator that, when acting on a quantum particle(s) wave function, gives you the allowed energies of that quantum state.

what is the quantum model: probability

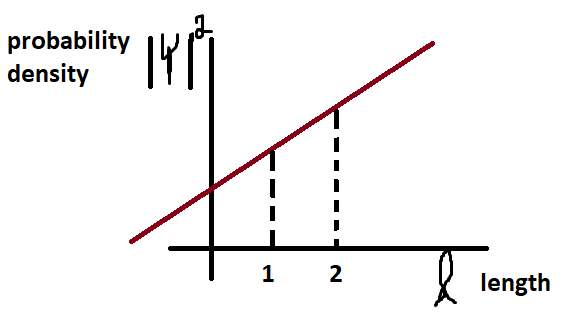
The wave function of a particle by itself gives you no information whatsoever. On the contrary, however, when the Hamiltonian acts on it, you obtain the wave function’s allowed energies. Additionally, when you square the wave function, it yields the quantum particles’ probability density. Don’t let the probability density term throw you off. It just means the probability divided by the length. As an example, if the density is 2x+1, it means 2x+1/picometer.

I graphed the probability density vs length in the above graph. Between 1 & 2, the area under the graph is bigger than under 0 & 1. This means that there is more of a chance of finding the particle in that area than under 0 and 1. Click here for more information on the topic.